Meaning of measure scales

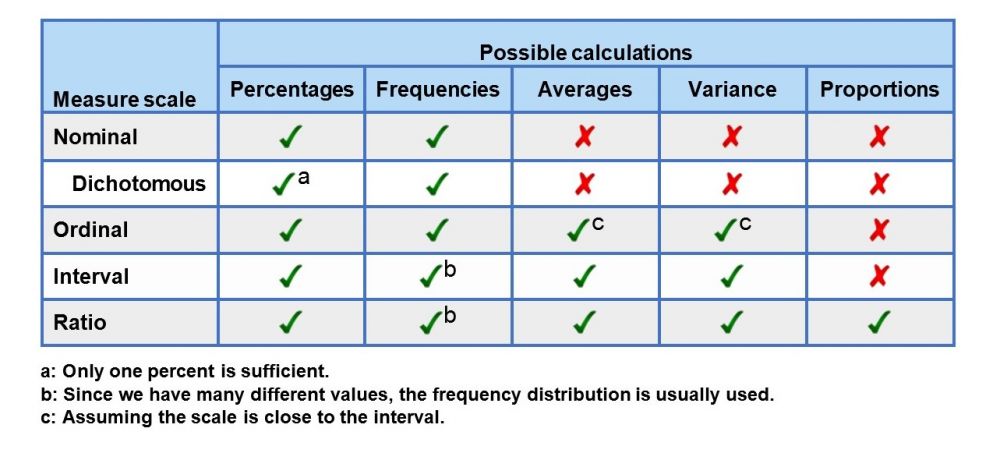
Table: computations in 1KA

To calculate averages and variances, the measurement scale must be at least interval, and for the computations of proportions, it must be at least ratio scale. For averages and variances, the ordinal scale is sufficient, in case we assume that the differences between the categories are the same (see point 2).

1. NOMINAL MEASURE SCALE

For variables with a nominal scale, data is classified into categories without any special order or structure (e.g. regions, clients, religions), so we cannot determine the order, averages and ratios.

In 1KA analyses in the case of nominal measurement scales, the calculation of averages is not shown.

1.1. Dichotomous scale

This particular type of nominal scale has only two categories (e.g. yes/no, male/female…). Here we also cannot determine order, averages and ratios.

For dichotomous variables, the analysis is further simplified by presenting the results with only 1 % (e.g., we say the proportion of women and we do not need to mention the proportion of men).

2. ORDINAL MEASURE SCALE

In the ordinal scale, the values can be compared (larger, smaller), but the distances between adjacent categories can vary greatly. An example is the time of skiing – there is a hundredth of a second difference between the 1^st and 2^nd places, and a second between the 2^nd and 3^rd places. Nevertheless, an ordinal scale is suitable for measuring certain phenomena, e.g. in social sciences, where we assume that the differences between the categories are the same (for example, on a scale from 1 to 5, the difference between 2 and 3 is equal to the difference between 4 and 5). In the social sciences, Likert’s scale 1-5 (satisficing, agreement, liking…) is especially popular, taking into account the methodological recommendation.

Assuming that the differences between the categories are the same, we can calculate the average and the variance in the case of an ordinal scale, as we approach the interval scale. Due to the prevailing opinion scales, the ordinal scale in social sciences is the most common.

In 1KA, categorical questions with one possible answer are defined by default as ordinal variables if they contain 4 or more possible answers. Otherwise, the default setting is the nominal type of the variable. In 1KA, we can manually turn on the computation of averages by defining the variable as ordinal in the advanced editing options of the question.

3. INTERVAL MEASURE SCALE

For variables with an interval scale, the distance between the values is the same. Because the size of the scale and point zero depend on our choice, the scale does not have an absolute zero. For the phenomena that we are studying with this scale, we can determine what is greater than something else and for how much – we can compare the differences between the values. An example may be a temperature where the difference between 10 ° C and 11 ° C is equal to 11 ° C and 12 ° C, but 20 ° C is not “twice as warm” as 10 ° C. Similar properties have the IQ scales, where the difference between 100 and 10 is comparable to the difference between 110 and 120, but it cannot be said that the 120 IQ is twice as high as 60.

For interval variables, we can calculate averages and variance.

4. RATIO MEASURE SCALE

In addition to the fact that the distances between the values are the same, absolute zero can be determined for variables with a scale of dimensions so the distance between the values reflects the actual differences. An example can be the measurement of length in meters, where the significance of the zero value is clearly determined. The value of 2 meters is thus 2 times longer than 1 meter. Additional examples include age (40 years and 20 years) and income (2000 € to 1000 €). As can be seen from the examples, based on this scale, we can compare the ratios between values. In sociological research, the use of ratio scales is less frequent.

In terms of variables, we can calculate averages, variance and ratios.

<< Back to Basic Recommendations